Universitas Sulawesi Barat (Unsulbar) Majene adalah salah satu Perguruan Tinggi Negeri (PTN) di Indonesia, dan merupakan satu-satunya Perguruan Tinggi Negeri (PTN) di Sulawesi Barat. Belakangan ini terjadi konflik dualisme di Perguruan Tinggi ini. Saya sebagai mahasiswa di kampus ini, merasa tidak nyaman dengan adanya perselisihan antar dua kelompok ini. Terlepas dari masalah konflik dualisme ini, kita harus melihat sisi baik dari Unsulbar. Status Unsulbar kini sudah menjadi Perguruan Tinggi Negeri (PTN) yang dimana penegeriannya butuh kerja keras. Dan ternyata Program Studi di Unsulbar juga sudah terakreditas oleh Ban-PT walaupun tidak semuanya. Berikut daftar program studi yang terakreditas :

 

DALAM MENYELESAIKAN PERSAMAAN DIFERENSIAL

LINIER HOMOGEN ORDE-n 

Lester Randolph Ford, Sr adalah Matematikawan asal Amerika yang lahir tahun 1886 . Ford menerima gelar Phd Matematika dari Unvirsitas Harvard pada tahun 1917. Pada tahun 1938, dia menuliskan artikel berjudul “Pecahan” di Jurnal matematika American Mathematical Monthly, volume 45, nomer 9, halaman 586-601. Di artikel tersebut Ford menjelaskan bagaimana bentuk pecahan p/q direpresentasikan ke bentuk Lingkaran. Nah lingkaran yang merupakan representasi dari pecahan inilah yang disebut Lingkaran Ford.

Definisi: Diberikan pacahan p/q dalam bentuk paling sederhana. Lingkaran ford dari p/q  dintoasikan C[p/q] pada bidang-xy adalah lingkaran dengan titik pusat (p/q, 1/2q² ) dan jari-jari 1/2q².

 contoh: C[1/2] mempunyai titik pusat di ( 1/2, 1/8) dan jari-jari 1/8.

Dari definsi terlihat ordinat dari titik pusat dan jari-jarinya sama, itu berarti lingkaran ford bersinggungan dengan sumbu x. So lingkaran-lingkaran ford akan berjejer tepat diatas sumbu x. Nah… yang menarik lingkaran-lingkaran  ford mustahil berpotongan.

Teorema: Dua lingkaran ford dari 2 pecahan berbeda tidak pernah berpotongan. Keduanya akan bersinggungan atau terpisah jarak antara satu-sama lain.

Selain itu teorema yang menarik dari Lingkaran Ford adalah

Teorema: Diberikan C[a/b] dan C[c/d] dua lingkaran ford yang bersinggungan maka lingkaran ford terbesar yang terletak diantara keduanya adalah C[(a+c)/(b+d)]

 

Dua soal tersebut saya berikan kepada siswa-siswa baru kelas X di sekolah saya mengajar. Semuanya bisa menjawab soal no. 1 tetapi tidak ada satupun yang bisa menjawab soal no .2, padahal soal no.2 adalah soal pengetahuan umum, sesuatu yang dianggap lebih mudah daripada Matematika. Saya yakin kalian meminta bantuan mbah Google untuk menjawab soal no.2 kecuali kalian tinggal di Kalimantan Utara.

Tujuan saya memberikan dua soal tesebut adalah ingin menunjukkan kepada para siswa baru bahwa matematika tidaklah sesulit yang mereka bayangkan. Saya tidak mengatakan matematika itu mudah tetapi saya pastikan, matematika tidaklah seseram yang kalian bayangkan. Tan Malaka ( Buat yang belum tahu siapa dia, googling saja. Bagi saya dia adalah pahlawan terkeren yang dimiliki Indonesia) justru mengatakan Matematika adalah pelajaran termudah dibandingkan pelajaran lain.

Sebenarnya matematikalah yang paling gampang kalau dibandingkan dengan sains yang lain, yaitu bagi mereka yang berpikir logis dan cerdik memakai cara. Bagi mereka semacam ini, tak perlu banyak menghafalkan. Sedangkan ilmu-ilmu lain, seperti ilmu bumi dan sejarah, perlu hafal menghafal berulang-ulang. Acapkali buktinya tak terorganisir dan tidak umum layaknya matematika dan ilmu alam. Untuk matematika, cukup kalau teori yang tak seberapa banyak itu dipegang dan terutama sekali berpegang teguh pada cara berpikir seperti yang sudah diuraikan. Berbeda dengan ilmu-ilmu lain, matematika sangat teratur tingkatnya, dari yang paling mudah ke yang sedikit lebih susah, dari sedikit susah ke tingkat sedikit lebih tinggi, begitulah terus sampai ke puncak setinggi-tingginya. Bagi pemuda yang berdarah logis dan cerdik, maka sekalian tingkat itu bisa dinaiki dengan gampang. Tidak sadar mereka tiba-tiba sudah sampai ke puncak.

-Madilog, Tan Malaka-

Dibandingkan pelajaran lain, matematikalah yang menghapalnya paling sedikit.  Hal utama dalam matematika adalah berpikir, inilah inti dari matematika. Mungkin, kamu akan berkomentar saya lebih suka menghapal daripada berpikir. Yang membedakan manusia dengan adalah berpikir. Kalau sekedar menghapal burung Beo juga bisa menghapal. Burung Beo sanggup menghapal puluhan kata dan kalimat tetapi tidak bisa berpikir apa maknanya. Tujuan sekolah adalah membuat manusia berpikir, so.. untuk apa susah-susah sekolah kalau kamu masih alergi dengan berpikir.

Sumber  : http://ariaturns.wordpress.com/

Definisi: Diberikan ,elemen  dilatakan elemen maksimal jika TIDAK ADA   sedemikian hingga .

Jadi elemen 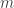dalam suatu poset dikatakan maksimal jika tidak ada elemen lain yang lebih besar dari 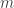. Dengan kata lain  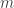 adalah elemen maksimal jika tidak lebih kecil dari semua elemen di suatu Poset.

Sekarang kita bahas elemen maksimum

Definisi: Diberikan ,elemen  dilatakan elemen maksimum atau disebut juga  elemen terbesar jika untuk semua   berlaku 

Sesuai dengan namanya elemen maksimun adalah elemen tersebar, artinya semua elemen didalam poset akan selalu lebih kecil atau sama dengan elemen maksimun tersebut.

Sekarang kita masuk ke contoh, supaya lebih jelas

Contoh 1: Diberikan poset   dengan  dan relasi urutan  yang didefinisikan (yaitu membagi ), untuk .

Dari contoh 1, bilangan 6,7,8,9 dan 10 adalah elemen maksimal, karena tidak ada bilangan di yang dapat dibagi oleh  6,7,8,9 dan 10 kecuali oleh diri mereka sendiri. Selanjutnya, apa elemen maksimumnya? Tidak ada, poset   tidak mempunyai elemen maksimum, karena tidak ada bilangan di yang dapat dibagi oleh semua bilangan pada himpunan tersebut.

Contoh 2:  Diberikan poset   dengan  dan relasi urutan  yang didefinisikan (yaitu membagi 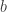), untuk .

Bilangan 256 merupakan elemen maksimum sekaligus maksimal pada . Mengapa?

Kebalikan dari maksimal adalah minimal

Definisi: Diberikan , elemen  dilatakan elemen minimal jika TIDAK ADA   sedemikian hingga .

Jadi elemen dalam suatu poset dikatakan minimal jika tidak ada elemen lain yang lebih kecil dari . Dengan kata lain   adalah elemen minimal jika tidak lebih besar dari semua elemen di suatu Poset.

Sedangkan elemen minimum merupakan kebalikan dari elemen maksimum

Definisi: Diberikan ,elemen  dilatakan elemen minimum atau disebut juga elemen terkecil jika untuk semua   berlaku .

Suatu elemen pada poset dikatakan mimimum atau terkecil, jika untuk semua eleme pada poset tersebut akan selalu lebih besar atau sama dengan elemen minimum tersebut

Pada contoh 1, bilangan 2 dan 3 merupakan elemen minimal, karena tidak ada bilangan di yang merupakan faktor dari 2 dan 3 kecuali diri mereka sendiri. Poset   tidak mempunyai elemen minimum, karena tidak ada bilangan di yang menjadi faktor dari semua bilangan pada himpunan tersebut.

Sedangkan pada contoh 2, bilangan 2 adalah elemen minimum sekaligus minimal. Mengapa?

Dari apa yang sudah kita bahas dapat disimpulkan sebagai berikut

Bagaimana kalian sudah jelas bendanya maksimal dengan maksimum dan minimal dengan minimum, atau malah tambah bingung :)

Sumber : http://ariaturns.wordpress.com/