Posted by : GLOBAL EDUCARE
Tuesday, September 2, 2014
Maksimal vs Maksimum
Definisi: Diberikan  ,elemen
,elemen  dilatakan elemen maksimal jika TIDAK ADA
dilatakan elemen maksimal jika TIDAK ADA  sedemikian hingga
sedemikian hingga  .
.
Jadi elemen 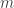 dalam suatu poset dikatakan maksimal jika tidak ada elemen lain yang lebih besar dari
dalam suatu poset dikatakan maksimal jika tidak ada elemen lain yang lebih besar dari 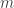 . Dengan kata lain
. Dengan kata lain 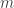 adalah elemen maksimal jika tidak lebih kecil dari semua elemen di suatu Poset.
adalah elemen maksimal jika tidak lebih kecil dari semua elemen di suatu Poset.
Sekarang kita bahas elemen maksimum
Definisi: Diberikan  ,elemen
,elemen  dilatakan elemen maksimum atau disebut juga elemen terbesar jika untuk semua
dilatakan elemen maksimum atau disebut juga elemen terbesar jika untuk semua  berlaku
berlaku 
Sesuai dengan namanya elemen maksimun
adalah elemen tersebar, artinya semua elemen didalam poset akan selalu
lebih kecil atau sama dengan elemen maksimun tersebut.
Sekarang kita masuk ke contoh, supaya lebih jelas
Contoh 1: Diberikan poset  dengan
dengan  dan relasi urutan
dan relasi urutan  yang didefinisikan
yang didefinisikan  (yaitu
(yaitu  membagi
membagi  ), untuk
), untuk  .
.
Dari contoh 1, bilangan 6,7,8,9 dan 10 adalah elemen maksimal, karena tidak ada bilangan di  yang dapat dibagi oleh 6,7,8,9 dan 10 kecuali oleh diri mereka
sendiri. Selanjutnya, apa elemen maksimumnya? Tidak ada, poset
yang dapat dibagi oleh 6,7,8,9 dan 10 kecuali oleh diri mereka
sendiri. Selanjutnya, apa elemen maksimumnya? Tidak ada, poset  tidak mempunyai elemen maksimum, karena tidak ada bilangan di
tidak mempunyai elemen maksimum, karena tidak ada bilangan di  yang dapat dibagi oleh semua bilangan pada himpunan tersebut.
yang dapat dibagi oleh semua bilangan pada himpunan tersebut.
Contoh 2: Diberikan poset  dengan
dengan  dan relasi urutan
dan relasi urutan  yang didefinisikan
yang didefinisikan  (yaitu
(yaitu  membagi
membagi 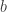 ), untuk
), untuk  .
.
Bilangan 256 merupakan elemen maksimum sekaligus maksimal pada  . Mengapa?
. Mengapa?
Minimal vs Minimum
Kebalikan dari maksimal adalah minimal
Definisi: Diberikan  , elemen
, elemen  dilatakan elemen minimal jika TIDAK ADA
dilatakan elemen minimal jika TIDAK ADA  sedemikian hingga
sedemikian hingga  .
.
Jadi elemen  dalam suatu poset dikatakan minimal jika tidak ada elemen lain yang lebih kecil dari
dalam suatu poset dikatakan minimal jika tidak ada elemen lain yang lebih kecil dari  . Dengan kata lain
. Dengan kata lain  adalah elemen minimal jika tidak lebih besar dari semua elemen di suatu Poset.
adalah elemen minimal jika tidak lebih besar dari semua elemen di suatu Poset.
Sedangkan elemen minimum merupakan kebalikan dari elemen maksimum
Definisi: Diberikan  ,elemen
,elemen  dilatakan elemen minimum atau disebut juga elemen terkecil jika untuk semua
dilatakan elemen minimum atau disebut juga elemen terkecil jika untuk semua  berlaku
berlaku  .
.
Suatu elemen pada poset dikatakan mimimum
atau terkecil, jika untuk semua eleme pada poset tersebut akan selalu
lebih besar atau sama dengan elemen minimum tersebut
Pada contoh 1, bilangan 2 dan 3 merupakan elemen minimal, karena tidak ada bilangan di  yang merupakan faktor dari 2 dan 3 kecuali diri mereka sendiri. Poset
yang merupakan faktor dari 2 dan 3 kecuali diri mereka sendiri. Poset  tidak mempunyai elemen minimum, karena tidak ada bilangan di
tidak mempunyai elemen minimum, karena tidak ada bilangan di  yang menjadi faktor dari semua bilangan pada himpunan tersebut.
yang menjadi faktor dari semua bilangan pada himpunan tersebut.
Sedangkan pada contoh 2, bilangan 2 adalah elemen minimum sekaligus minimal. Mengapa?
Dari apa yang sudah kita bahas dapat disimpulkan sebagai berikut
- Elemen maksimal dan mimimal tidak harus tunggal
- Elemen maksimum dan minimum tunggal
- Elemen maksimum dengan sendirinya merupakan elemen maksimal, begitupula elemen minimum adalah elemen minimal, tetapi sebaliknya tidak berlaku.
Bagaimana kalian sudah jelas bendanya maksimal dengan maksimum dan minimal dengan minimum, atau malah tambah bingung :)
Sumber : http://ariaturns.wordpress.com/
Sumber : http://ariaturns.wordpress.com/
Related Posts :
- Back to Home »
- Matematika »
- Maksimal, Maksimum, Minimal, Minimum, Apa bedanya?









